Cara menyederhanakan bentuk akar berpangkat sebenarnya tidak sesulit kelihatannya. Untuk menyederhanakan akar kuadrat, Anda harus memfaktorkan angkanya dan menarik akar kuadrat dari kuadrat sempurna di bawah tanda akar, dan berikut beberapa ulasan lengkap dengan contohnya.
Salah satu cara menyederhanakan bentuk akar berpangkat yaitu dengan memahami terlebih dahulu mengenai faktor. Tujuan cara sederhanakan bentuk akar pangkat yaitu menuliskannya dalam bentuk yang mudah dipahami dan digunakan dalam soal matematika.
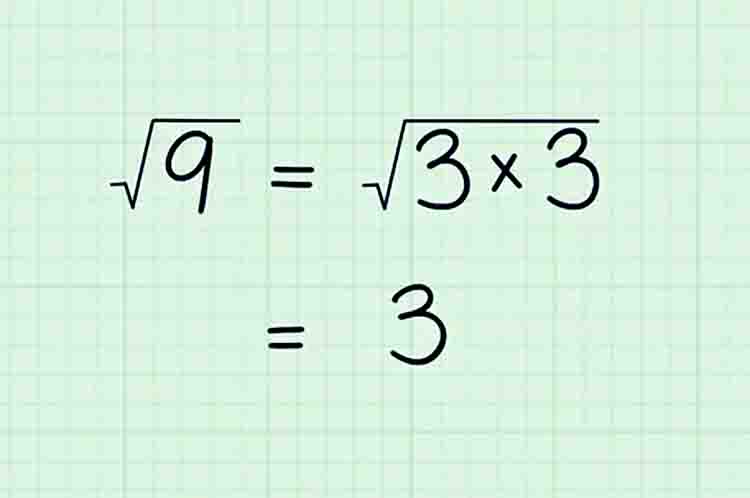
1. Menyederhanakan Akar Kuadrat dengan Memfaktorkan – Cara menyederhanakan bentuk akar berpangkat pertama
Salah satu cara menyederhanakan bentuk akar berpangkat yaitu dengan memahami terlebih dahulu mengenai faktor. Tujuan cara sederhanakan bentuk akar pangkat yaitu menuliskannya dalam bentuk yang mudah dipahami dan digunakan dalam soal matematika.
Dengan memfaktorkan, angka besar akan dipecahkan menjadi dua atau lebih angka “faktor” lebih kecil, example mengubah 9 menjadi 3×3.
Setelah Anda menemukan faktor ini, Anda dapat menuliskan kembali akar kuadrat dalam bentuk yang lebih sederhana. Terkadang bahkan mengubahnya menjadi sebuah bilangan bulat biasa. Example, √9 = √(3×3) = 3.
2. Membagi Angka dengan Bilangan Prima Terkecil yang Mungkin – Cara menyederhanakan bentuk akar berpangkat kedua
Jika angka yang berada di bawah tanda akar merupakan bilangan genap, bagi dengan 2. Maka jika angka ganjil, maka cobalah bagi dengan angka 5. Jika tidak satupun dari pembagian ini memberikan Anda hasil bilangan bulat.
Cobalah angka selanjutnya, lalu bagi dengan setiap bilangan prima hingga mendapatkan bilangan bulat sebagai hasilnya.
Anda hanya perlu menguji bilangan prima saja, karena semua angka yang lain memiliki bilangan prima sebagai faktornya. Example, Anda tidak perlu menguji dengan 4, karena semua angka yang bisa dibagi 4 juga bisa dibagi 2.
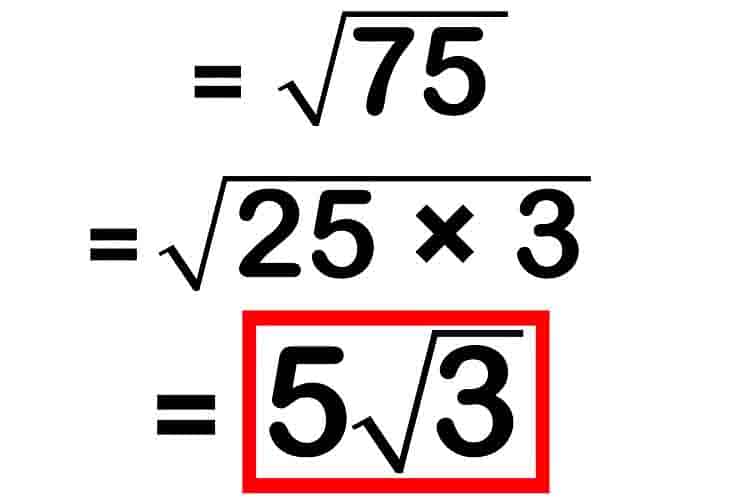
3. Tulis Ulang Akar Kuadrat Sebagai Soal Perkalian – Cara menyederhanakan bentuk akar pangkat ketiga
Tetap tuliskan perkalian ini di bawah tanda akar, dan jangan lupa untuk menyertakan kedua faktornya. Example, jika Anda mencoba menyederhanakan √98, Ikuti langkah untuk menemukan bahwa 98 ÷ 2 = 49, jadi 98 = 2×49. Tulis lagi angka 98 dalam bentuk akar kuadrat aslinya menggunakan informasi ini: √98 = √(2 x 49).
4. Ulangi Pada Salah Satu Angka yang Tersisa – Cara menyederhanakan bentuk akar berpangkat keempat
Sebelum Anda mengetahui cara menyederhanakan bentuk akar berpangkat kuadrat, Anda harus memfaktorkannya hingga menjadi dua angka yang sama persis.
Hal ini masuk akal jika Anda ingat apa arti akar kuadrat: angka √(2 x 2). Berarti angka yang Anda bisa kalikan dengan dirinya sendiri sama dengan 2 x 2. Tentu saja, jawabannya yaitu 2.

5. Selesaikan dengan Mengeluarkan Sebuah Bilangan Bulat – Cara menyederhanakan bentuk akar pangkat kelima
Setelah Anda memecahkan soal menjadi dua faktor yang sama persis. Anda bisa mengubahnya ke dalam bilangan bulat biasa di luar tanda akar. Biarkan sisa faktor lain tetap disimpan dalam akar kuadrat. Example, √(2 x 7 x 7) = √(2)√(7×7) = √(2) x 7 = 7√(2).
6. Kalikan Seluruh Bilangan Bulat Jika Ada Lebih dari Satu – Cara sederhanakan bentuk akar pangkat keenam
Pada beberapa angka akar kuadrat yang besar, Anda bisa menyederhanakan lebih dari sekali. Jika hal ini terjadi, kalikan bilangan bulat yang Anda dapatkan untuk mendapatkan jawaban akhirnya.
7. Tulis “Tidak Dapat Disederhanakan” Kalau Tidak Ada Dua Faktor yang Sama – Cara menyederhanakan akar pangkat ketujuh
Beberapa angka akar kuadrat telah berada dalam bentuk yang paling sederhana. Jika Anda terus memfaktorkan hingga semuanya berupa bilangan prima. Dan tidak ada satu pasang yang sama, maka tidak ada yang bisa Anda lakukan. Anda mungkin diberi soal jebakan.
8. Mengenali Kuadrat Sempurna – Cara menyederhanakan akar berpangkat kedelapan
Ingatlah beberapa angka kuadrat sempurna. Mengkuadratkan suatu angka, atau mengalikannya dengan angka itu sendiri, akan membuat angka kuadrat sempurna. Example, 25 adalah angka kuadrat sempurna, karena 5 x 5, atau 52, sama dengan 25.
Ingatlah paling tidak sepuluh angka kuadrat sempurna pertama untuk membantu Anda mengenali. Dan mengetahui cara menyederhanakan bentuk akar berpangkat kuadrat sempurna.

9. Cari Akar Kuadrat Dari Kuadrat Sempurna – Tips membuat lebih sederhana bentuk akar berpangkat kesembilan
Jika Anda mengenali kuadrat sempurna di bawah tanda akar, Anda bisa mengubahnya menjadi akar kuadrat dan mengeluarkannya dari (√). Example, jika Anda melihat angka 25 di bawah tanda akar, jawabannya adalah 5, karena 25 adalah kuadrat sempurna.
10. Faktorkan Angka ke Dalam Kuadrat Sempurna – Cara bikin simple bentuk akar berpangkat kesepuluh
Manfaatkanlah kuadrat sempurna saat melanjutkan metode faktor saat menyederhanakan akar kuadrat. Jika Anda menyadari adanya faktor dari kuadrat sempurna, maka Anda akan lebih cepat dan lebih mudah menyelesaikan soal.
Example, √50 = √(25 x 2) = 5√2. Jika kedua angka terakhir dari sebuah angka berakhiran 25, 50, atau 75, Anda bisa memfaktorkan 25 dari angka tersebut.

11. Faktorkan Sejumlah Angka dengan Lebih dari Satu Kuadrat – Cara menyederhanakan akar berpangkat kesebelas
Jika faktor dari angka mempunyai lebih dari satu kuadrat sempurna, keluarkan semuanya dari dalam tanda akar. Jika Anda mendapatkan beberapa kuadrat sempurna dalam proses penyederhanaan akar kuadrat. Pindahkan semua akar kuadratnya ke luar tanda √ lalu kalikan seluruhnya.
Baca juga:
- 2 Cara Menulis Daftar Pustaka Dari Jurnal dengan Penulisan Yang Baik
- Pulau Bintan Merupakan Tempat Pertambangan dari 9 Mineral Berikut
- Memiliki Banyak Keunikan, Inilah 11 Nama Sungai di Pulau Jawa
- 7 Urutan Member NCT Tertampan, Setujukah NCTzen?
Cara menyederhanakan bentuk akar berpangkat berbeda dengan menghitung nilainya. Tidak ada satupun tips menyederhanakan akar pangkat yang mengharuskan Anda mendapatkan angka dengan desimal di dalamnya. Pure mathematics is logical poetic ideas.



